Area Of A Sector Of A Circle Formula Calculator

In geometry, circle sector is a part of a circle lying between two straight lines drawn from the centre to the edge. The formula, solved example & step by step calculations may useful for users to understand how the input values are being used in such sector area calculations. Also this featured sector area calculator uses the various conversion functions to find its volume in SI or metric or US customary units.

Circles are everywhere in the real world, which is why their radii, diameters and circumference are significant in real life applications. But there are other parts of circles – sectors and angles, for instance – that also have importance in everyday applications as well. For these reasons and more, geometry also has equations and problem calculations dealing with central angles, arcs and sectors of a circle. A simple closed shape where all points in a plane are at a given distance from a given point, the centre, is called a circle. The distance from the centre to the outside edge of the circle is called the radius.

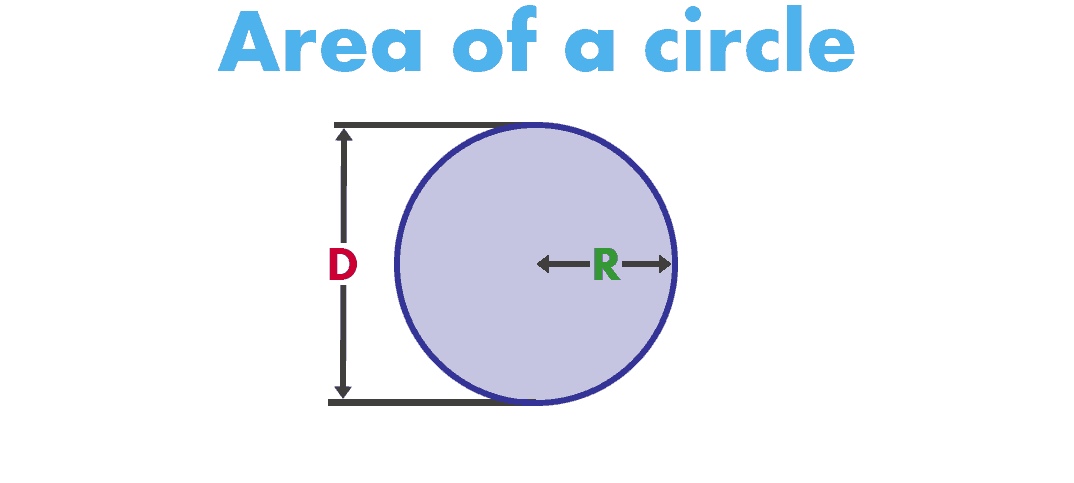
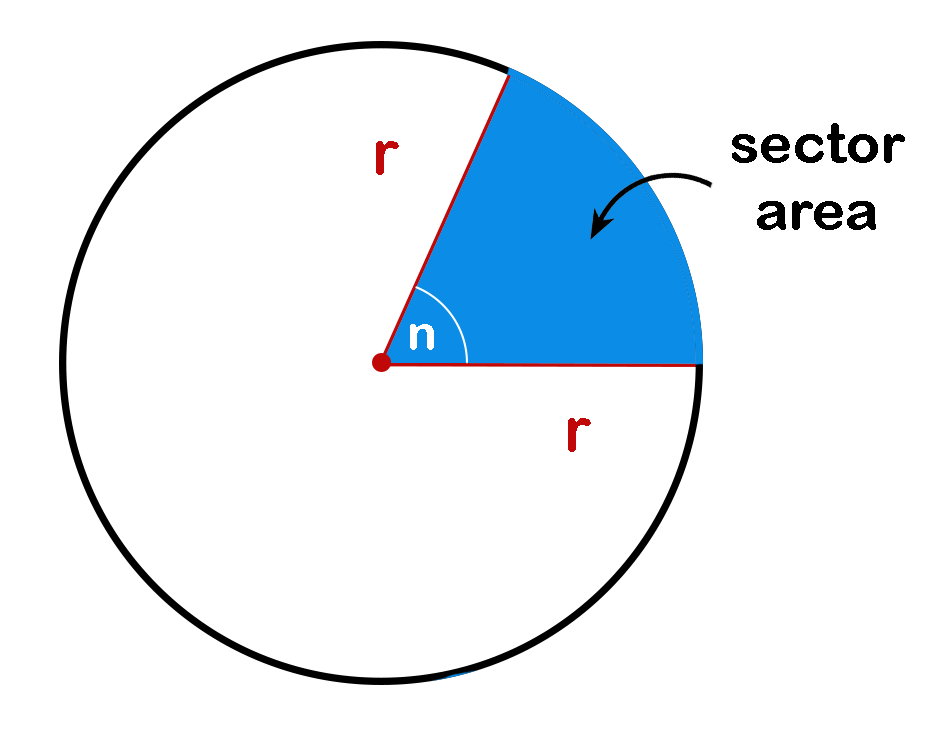
The formula by which the area of a circle is calculated is - Pir2, where Pi is the universal constant which is 3.14 and r is the radius. You can also calculate the area of the sector of a circle. The sector is an area that is enclosed by two radii and an arc. The area of the sector of a circle can be calculated by using the formula - (Q/360º) × Pir2, where Q is the angle subtended at the centre, measured in degrees.

Angles are measured in degrees, but sometimes to make the mathematics simpler and elegant it's better to use radians which is another way of denoting an angle. A radian is the angle subtended by an arc of length equal to the radius of the circle. ( "Subtended" means produced by joining two lines from the end points of the arc to the center). In the field of area & volume calculations, finding the sector area of a circle is important to understand basic mathematical computations.

There are two types of sectors, minor and major sector. A minor sector is less than a semi-circle sector, whereas a major sector is a sector that is greater than a semi-circle. Central angles are particularly relevant when it comes to evenly dividing up pizza, or any other circular-based food, among a set number of people.

Say there are five people at a soiree where a large pizza and a large cake are to be shared. What is the angle that both the pizza and the cake have to be divided at to ensure an equal slice for everyone? You will instantly get the area of sector with the step by step demonstration of the calculation. It also shows the formula that it used to find the sector of circle. Sector area calculator only finds the inner portion of circle. If you want to calculate the circumference of circle, you can use ourcircumference calculatoranytime.

The following mathematical formula is used in this circular sector calculator to find the area for the given input values of radius r & the angle θ in degrees. The measure of the central angle or the length of the arc. The central angle is the angle subtended by an arc of a sector at the center of a circle. The central angle can be given in degrees or radians.

Anytime you cut a slice out of a pumpkin pie, a round birthday cake, or a circular pizza, you are removing a sector. A sector is created by the central angle formed with two radii, and it includes the area inside the circle from that center point to the circle itself. The portion of the circle's circumference bounded by the radii, the arc, is part of the sector. The area of a sector of a circle is the amount of space enclosed within the boundary of the sector.

A sector always originates from the center of the circle. The sector of a circle is defined as the portion of a circle that is enclosed between its two radii and the arc adjoining them. The semi-circle is the most common sector of a circle, which represents half a circle.

Let us learn more about the area of sector, its formula, and how to calculate the area of a sector using radians and degrees. Thus, a sector's area is equal to the radius r squared times the central angle θ in radians, divided by 2. Pies, cakes, pizzas; so many foods we eat neatly lend themselves to mathematics, because they are models of circles. Bits cut off by connecting any two points on the circle are segments.

Since both sectors and segments are part of a circle's interior, both have area. Unlike triangles, the boundaries of sectors are not established by line segments. The distance along that curved "side" is the arc length.

Acute central angles will always produce minor arcs and small sectors. When the central angle formed by the two radii is 90°, the sector is called a quadrant . When the two radii form a 180°, or half the circle, the sector is called a semicircle and has a major arc. You can use circumference formula calculator to solve circumference online.

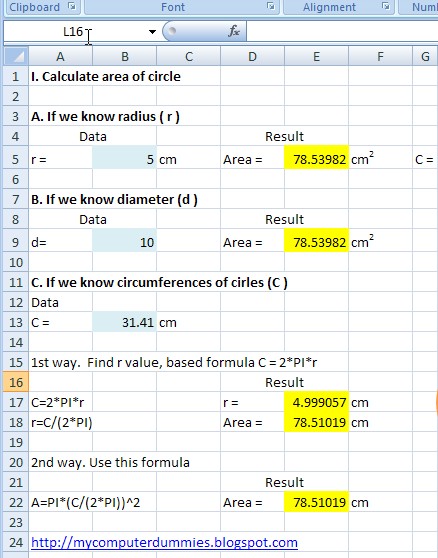
For manual calculations, let's assume we draw a circle of radius 3.5 centimeters. As we know this blue boundary of the circle will be its perimeter. The perimeter of the circle is also called circumference.

Getcalc.com's circle sector calculator is an online basic geometry tool to calculate area of sector & length of an arc , in both US customary & metric units. All you need is to know the radius of the circle and the number of degrees (α) that the circular sector occupies. When you have it, press the calculate button and you will get the result immediately. Circumference of a circle calculator works according to the above-given formula. You can find the circumference calculator useful to solve circumference online. Also try our cbm calculator to calculate triangles, cubic feet from length and width.

An online area of a sector calculator is specifically programmed to find the area of the sector, the arc length, and chord length of a circle sector. This free calculator generates accurate outputs so you may not feel any difficulty during your calculations. But before we move further, let us make sure that you need to memorize some crucial terms which are as follows. The area of a sector along an arc is also known as the circular sector. It's a percent or portion of a disk that is enclosed by that arc and two equal radii. To understand how to calculate the area of such a sector, it's important to understand the formula that it uses, which is given above.

The step by step workout for how to find what is area & length of a circle sector. Students may use this circle sector calculator to generate work with steps for any other similar input values. An ellipse looks like a circle but is not a circle and is the group of all points on a plane whose distance from two fixed points sum up to a constant. In an ellipse, you do not have a single radius but two different values. The values are taken from the centre to the two different edges of the ellipse called the semi-major and semi-minor axes.

The calculator calculates the area by using the formula - Pi X a X b; here a and b are the distances of the two axes. The following table gives the formulas for the area of sector and area of segment for angles in degrees or radians. Scroll down the page for more explanations, examples and worksheets for the area of sectors and segments. Please input radius of the circle and the central angle in degrees, then click Calculate Area of Sector button. The calculator will show you the chart of the sector based on your input as well. Find the radius of a sector whose area is 47 meters squared and central angle is 0.63 radians.

This tool can be used to solve geometry problems related tocircle. Moreover, it can be used to measure the land in sectors, and some cool things such slice of pizza or cake. The areas of both segments and sectors can be calculated in square units of whatever linear measurement you are given.

Once you know the radius, you have the lengths of two of the parts of the sector. You only need to know arc length or the central angle, in degrees or radians. Do you want to calculate the area of a circular sector? Use our online calculator and you will get the area of the sector automatically as well as its arc length and perimeter. Area of a sector is a fractions of the area of a circle.

Both can be calculated using the angle at the centre and the diameter or radius. Circumference formula calculator is simple and very easy to use. To calculate the circumference of a circle, just provide radius to our circumference calculator and get your answer. Our circumference to diameter calculator will show you diameter, circumference & area as the results. Let us use these formulas and learn how to calculate the area of the sector of a circle when the subtended angle is given in degrees with the help of an example.

Calculate the area of a sector using the central angle and radius below and learn the formula and steps to solve it below. The area of a sector is the region enclosed by the two radii of a circle and the arc. In simple words, the area of a sector is a fraction of the area of the circle. Use our online calculator to perform area of a sector of a circle calculation.

On this page you can calculate the properties of a circular sector. It is limited by two straight lines from its center. If, instead of a central angle in degrees, you are given the radians, you use an even easier formula. Rememberthis second one formula for calculating the area of the circular sector we will use it if we are given the angle expressed in radians.

If we look at the figure above these lines, the circular sector would correspond to the part colored in turquoise. It is formed by the rotation of the radius a given number of degrees or radians. Use a protractor to measure the central angle made by the two radii.

Set the base of the protractor along one of the radii, with the central point of the protractor aligned with the center of the circle. Then read the angle measurement that corresponds with the position of the second radius forming the sector. In some real world situations, you may not be able to measure the diameter or radius accurately. If the diameter is not drawn for you or the center is not identified, it can be difficult to approximate the center of a circle. A radian is the angle subtended by an arc of length equal to the radius of a circle.

Notice how the arc length and area formulas are based on the area and circumference formulas for a circle. Both are simply multiplied by the angle at the centre over 360 (this fraction 'cuts out' the part of the circle you're working with). Next, we will look at the formula for the area of a sector where the central angle is measured in radians. Recall that the angle of a full circle in radians is 2π. We can calculate the central angle subtended by a sector, given the area of the sector and area of circle. We can calculate the area of the sector, given the central angle and radius of circle.

It consists of a region bounded by two radii and an arc lying between the radii. The circumference is the distance around the outside of the circle denoted by . Circumference calculator allows you to calculate diameter, area & circumference online. The figure given below represents the sectors in a circle.

The shaded region shows the area of the sector OAPB. It should be noted that the unshaded region is also a sector of the circle. So, the shaded region is the area of the minor sector and the unshaded region is the area of the major sector.

We'll give you a tour of the most essential pieces of information regarding the area of a circle, its diameter, and its radius. We'll learn how to find the area of a circle, talk about the area of a circle formula, and discuss the other branches of mathematics that use the very same equation. If the sector's radius is 18 mm, find the central angle of the sector in radians. Calculate the area of a sector using the radius of an arc and the angle of rotation. This area uses units of degrees for the angle and any unit of distance for the radius. A minor sector of a circle is a sector that has the central angle of less than 180°.The measurement of the central angle of the minor sector cannot exceed 180°.

You can work out the length of an arc by calculating what fraction the angle is of the 360 degrees for a full circle. Circumference of the total circle made by the radius we know. Let's try an example where our central angle is 72° and our radius is 3 meters.

For the next question you are given the angle at the centre, 98 degrees, and the arc length, 10cm. To do this, write down the formula for the arc length, input the numbers you've been given and then solve the equation to find the value of x. Comparing the area of sector and area of circle, we get the formula for the area of sector when the central angle is given in radians. Find the fraction of the circle by putting the angle measurement of the sector over 360°, the total number of degrees in a circle. Comparing the area of sector and area of circle, we derive the formula for the area of sector when the central angle is given in degrees.